July 15, 2014
By Brad Miller, Ph.D.
 Can a Ransom Rest be used to measure recoil? Analysis of 3,500 rounds of .38 Special, 9mm Luger, .38 Super, .40 S&W, and .45 ACP ammunition shows that it can, and that it is surprisingly sensitive to small differences in handgun recoil.
Can a Ransom Rest be used to measure recoil? Analysis of 3,500 rounds of .38 Special, 9mm Luger, .38 Super, .40 S&W, and .45 ACP ammunition shows that it can, and that it is surprisingly sensitive to small differences in handgun recoil.
The Ransom Rest is a machine designed to test the mechanical accuracy of a handgun by holding it in the same position for each shot. A handgun attaches securely to the base of the Ransom Rest by an appendage known as the rocker arm. The rocker arm moves freely and pivots upward when the gun fires (Figure 1). Its movement is restricted by spring tension and steel and fiber friction discs. According to the manufacturer, the rocker arm "recoils as nearly like the human hand as possible."
 Given how the arm moves during recoil, and the mechanism of resistance that limits its movement, more recoil force should produce more movement. It does. But how sensitive is it to different loads? This was studied in the following statistical evaluation.
Given how the arm moves during recoil, and the mechanism of resistance that limits its movement, more recoil force should produce more movement. It does. But how sensitive is it to different loads? This was studied in the following statistical evaluation.
I tested whether the Ransom Rest could distinguish between different gunpowders. Some gunpowders produce more recoil because they require more charge weight to produce the same velocity. This can be explained by the principle of conservation of mass.
Advertisement
Recoil is an example of Newton's third law of motion that for every action there is an opposite and equal reaction. Recoil force is the product of mass and acceleration (F=ma; Force equals mass times acceleration) with reference to the weight and velocity of the bullet. The conservation of mass requires that the weight of the gunpowder must also be taken into account.The gunpowder's weight is added to the mass (m) of what comes out of the end of the barrel (the ejecta) in the form of gas along with the bullet. More gunpowder weight produces more gas, which adds to the recoil force even if the bullet's velocity is the same. This means if you compare two different gunpowders that produce the same velocity but require different charge weights, the one that requires a larger charge weight produces more recoil.
Procedure
The test used .38 Super ammunition with the same bullet but loaded with eight different gunpowders. The gunpowders spanned a broad range of burning rates from fast to slow. Three or four different charge weights were loaded with each gunpowder. Ten-shot strings were fired with each charge weight. Velocity was measured with a Shooting Chrony chronograph. The test gun was a customized Para Ordnance high capacity pistol with a five-inch Kart barrel.
Advertisement
Hardware
The gunpowders were Vihtavuori N320, Hodgdon Titegroup, Winchester 231, Hodgdon Longshot, Alliant Power Pistol, Hodgdon HS-6, Vihtavuori 3N38 and Accurate #7 loaded with Remington 115 grain JHP bullets in same-headstamp brass at 1.245" OAL. Every charge was weighed by hand to minimize variation. There were 25 different loadings, plus five "repeats" used as calibration loads. The calibration loads were run at various times during the session to test the consistency of the rocker arm's movement. This came to 30 different ten-shot strings for a total of 300 rounds.
Rocker arm movement was measured as shown in Figure 1. The ruler was positioned perpendicular to the Ransom Rest mounting board and the front of the frame dust cover was the measuring point.
The use of multiple charge weights also revealed that the rocker arm movement, as measured, is linear, just like the mathematical model of recoil. Linear means that the values are aligned along a straight, or mostly straight, line, indicating change at a constant rate. Linearity is a common feature of ballistics, which is evident in loading manuals that show charge weights in velocity increments, such as the Hornady and Sierra manuals. For example, a gunpowder might produce a 50 fps increase in velocity for every 0.3 grains added. These linear characteristics allow charge weight and rocker arm movement for a specific velocity to be calculated with linear regression.
I'll begin by showing how the test results look when my charge weight and velocity results are plugged into a mathematical formula that calculates recoil energy. This will illustrate how charge weight contributes to recoil according to the conservation of mass. Then we'll see how the Ransom Rest results fit that theoretical model.
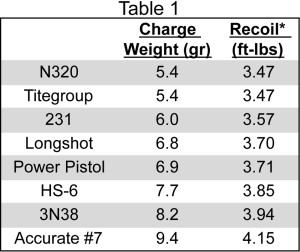 Let's start with some numbers. Table 1 shows the calculated charge weight and recoil energy for a velocity of 1275 fps. Most gunpowders required different charge weights to achieve the same velocity, and higher charge weights produced more recoil. Accurate #7 required 74% more weight than N320 and produced 20% more recoil for the same velocity
Let's start with some numbers. Table 1 shows the calculated charge weight and recoil energy for a velocity of 1275 fps. Most gunpowders required different charge weights to achieve the same velocity, and higher charge weights produced more recoil. Accurate #7 required 74% more weight than N320 and produced 20% more recoil for the same velocity
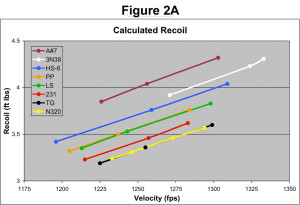 The calculated recoil profiles for each gunpowder are shown in a scatter plot in Figure 2A. The gunpowders with the lowest charge weights (N320 and Titegroup) produce the least recoil and are lowest on the plot. The gunpowder with the highest charge weight (Accurate #7) produced the most recoil and is highest on the plot. The calculated recoil of N320 and Titegroup are virtually the same and their profiles overlap. Longshot and Power Pistol powders are also very similar (see the values in Table 1).
The calculated recoil profiles for each gunpowder are shown in a scatter plot in Figure 2A. The gunpowders with the lowest charge weights (N320 and Titegroup) produce the least recoil and are lowest on the plot. The gunpowder with the highest charge weight (Accurate #7) produced the most recoil and is highest on the plot. The calculated recoil of N320 and Titegroup are virtually the same and their profiles overlap. Longshot and Power Pistol powders are also very similar (see the values in Table 1).
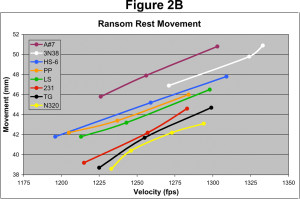 How does Ransom Rest movement compare to the calculated output? Rocker arm movement is shown in Figure 2B and it looks very much like the calculated results, perhaps better.
How does Ransom Rest movement compare to the calculated output? Rocker arm movement is shown in Figure 2B and it looks very much like the calculated results, perhaps better.
The gunpowder profiles are in the same general order as the calculated output, however, now all eight gunpowder profiles are separated. There is no longer any overlap between N320 and Titegroup, and Longshot and Power Pistol are more clearly separated. According to the Ransom Rest results, Accurate #7 produced 17% more recoil than N320, a value very close to the calculated 20%.
This demonstrates that Ransom Rest movement fits the theoretical model quite well. It can distinguish between gunpowders, which requires considerable sensitivity. Moreover, it is able to detect subtle differences between the real-world recoil characteristics of gunpowders that the mathematical formula can't address, as demonstrated by the distinct separation of N320 and Titegroup.
Precision Measurements
How precise is the rocker arm's movement? The extreme spread of movement in the 10-shot strings was small, ranging from one to five millimeters (mm). An example of the data is shown in Table 2. Look at the middle charge weight of 6.7 grains. The rocker arm moved from 42 to 45mm, a 3mm extreme spread, which was average (the average for all strings was 2.8mm). I want to emphasize an important point here: The extreme spread for 10 shots is only 3mm after having moved over 40mm. This indicates both consistency and precision in the rocker arm's movement.
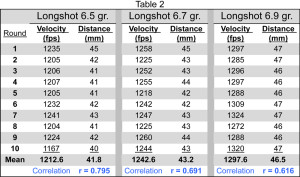 The data in Table 2 shows little overlap in the range of movement between the different charge weights. This was common, and affirms the consistency of the rocker arm's response to recoil.
The data in Table 2 shows little overlap in the range of movement between the different charge weights. This was common, and affirms the consistency of the rocker arm's response to recoil.
Movement data for each of the eight gunpowders was statistically tested with a one-way analysis of variance (ANOVA) (footnote 1). Tests for all eight gunpowders showed statistically significant differences (p < 0.0000001), which means the Ransom Rest's movement distinguished between the different charge weights.
Powder charges were separated by 0.1 grain (N320) and 0.2 grain (all others) increments. For example, I used three different charge weights with Winchester 231; 5.7, 5.9 and 6.1 grains. This produces two "adjacent" weight comparisons: one between 5.7 and 5.9 grains, and the other between 5.9 and 6.1 grains. There were 14 possible comparisons with 0.2 grain increments, and three comparisons for 0.1 grain increments, for a total of 17 adjacent comparisons.
Post-hoc t-test pairwise comparisons (footnote 1) were made between adjacent charge weights since the question was whether one can detect an increase in recoil with the next highest charge weight tested. Sixteen of the 17 comparisons showed statistically significant differences, indicating that the Ransom Rest distinguished between adjacent charge weights. The one comparison that was not statistically significantly different was between 5.4-grains and 5.5-grains of N320. In this case, more gunpowder did move the rocker arm more (0.9mm), just not quite enough to be statistically significantly different.
The statistical analysis confirms that the rocker arm could reliably distinguish between the incremental changes in charge weight with the same gunpowder. Only one comparison was not statistically significantly different, as noted.
The average distance between charge weights from all the data was 2.3mm. In the case of N320 with its 0.1 grains difference in charge weight, the average difference in movement was only 1.5mm, yet two of the three comparisons were statistically significantly different. Thus, the rocker arm's movement was precise enough to distinguish between relatively small differences in movement.
Sensitivity
The most important criterion is that there must be a positive correlation between rocker arm movement and velocity because more velocity means more recoil. This correlation is obvious when looking at the profiles on the scatter plot (Figure 2) where more charge weight produces more recoil, but this is on a large scale where there are measurable differences in charge weight.
What about on the micro-scale of the 10-shot string where the charge weight is the same?
Correlation statistics were used to assess this relationship. Correlation values can be positive or negative. A positive correlation indicates that the rocker arm movement and velocity go in the same direction — they both increase or both decrease. A negative correlation means that they go in opposite directions. Correlation values range from 1.0 (positive) to -1.0 (negative).
The size of the value determines whether the relationship is real or random, and the cutoff value depends on how many measurements are compared (sample size). The correlation cutoff value for a sample of ten is 0.549 (footnote 2). Correlation values of 0.549 and larger indicate that rocker arm movement distinguishes correctly between differences in velocity (recoil).
The correlation between velocity and rocker arm movement for each of the 30 strings of fire was calculated. The average of all 30 correlations was 0.643, higher than the cutoff value. Twenty-two of the correlations (73%) were greater than 0.549. See Table 2 for an example of the correlation data. All three of those 10-shot strings were significantly positively correlated.
The fact that the overwhelming majority of correlations (73%) were above the statistically significant cutoff value is strong evidence that the Ransom Rest's rocker arm movement is highly sensitive to small differences in velocity (recoil). Consider this: statistical theory predicts that only 5% of the correlations (1.5 of 30) would be above the cutoff value if the rocker arm movement did not correlate with recoil force, and they would be errors (false positives).
In addition, the present data is a replication of a previous test in which 96% of the 10-shot strings had correlations greater than 0.549. A high correlation between velocity and rocker arm movement is common. A quick look at data from over 1,000 rounds of .38 Special, 9mm Luger, .40 S&W and .45 ACP showed that 84% of 10-shot strings had a statistically significant positive correlation between rocker arm movement and velocity.
One possible reason why some correlations are below the cutoff value is because of the small extreme spread of range of movement. The correlations that were not statistically significant usually had a smaller extreme spread (average 2mm). Consistent with this interpretation is that larger extreme spreads of movement had higher correlation values. This hypothesis is supported by data from my other experiments that show the same trend.
Consistency / Repeatability
How consistent is the rocker arm's response to the same load tested at different times?
Some of the data points of three gunpowders in Figure 2 were averages of multiple 10-shot strings (calibration loads). The individual 10-shot string values are plotted in Figure 3 along with the averaged values to illustrate the variation in the rocker arm movement to the same loads. In the case of 231, the upper charge weight was an average of four separate 10-shot strings. The average value is connected with the line, and the separate strings are shown as unattached dots. The same applies for the two 10-shot strings of Titegroup's and 3N38's middle charge weights.
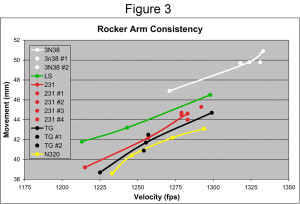 The four 231 strings did not encroach on the adjacent profiles of Longshot and Titegroup, and the two 3N38 movement averages only varied by 0.1 mm of movement. However, the average movement values of Titegroup's 10-shot strings were more widely spread and crossed the adjacent 231 and N320 profiles. This shows that there is some variation in the rocker arm's movement to the same load. The movement variation is not necessarily correlated with velocity differences between the strings based on this data and other calibration loads that I've analyzed, thus it might represent random variation in the rocker arm's behavior.
The four 231 strings did not encroach on the adjacent profiles of Longshot and Titegroup, and the two 3N38 movement averages only varied by 0.1 mm of movement. However, the average movement values of Titegroup's 10-shot strings were more widely spread and crossed the adjacent 231 and N320 profiles. This shows that there is some variation in the rocker arm's movement to the same load. The movement variation is not necessarily correlated with velocity differences between the strings based on this data and other calibration loads that I've analyzed, thus it might represent random variation in the rocker arm's behavior.
In the present example, the variation was not large, since the distance between Titegroup's two averages was 1.6mm after an average movement of 41.7mm. This represents an error of only +/- 2% of its total movement. The maximum distance between 231's four strings was 1.3mm for an error of +/- 1.4%.
This small degree of variation means that the Ransom Rest might have difficulty distinguishing between loads with similar recoil, though in this case the end result showed clear separation of the gunpowders. This emphasizes the advantage of using multiple charge weights for each gunpowder. The juxtaposition of the plotted recoil profiles delineates their relationship.
The reason(s) for the variation is not well understood. It might be related to ambient temperature, or some other factor. I have not specifically tested possible causes, so the source has yet to be determined.
Consistency is an issue for loads that are very similar in recoil force, because minor variations in response could result in overlapping profiles, but it is less of a concern for loads with larger differences. In any case, multiple charge weights, repeating strings at different times during a test session (calibration tests), or larger strings of fire can provide more confidence in the results.
Summary
The evidence overwhelmingly shows that the Ransom Rest can distinguish recoil with surprising precision. It does not measure recoil force in traditional units like foot-pounds. Instead, it measures "relative" recoil based on how far the rocker arm moves. It can discriminate between small differences in powder charge, as little as 0.1 grains, and it can distinguish between different gunpowders.
The clear correlation between velocity and rocker arm movement in individual 10-shot strings demonstrates how sensitive it is to small differences in recoil. The data presented here and the analysis of several thousand rounds of ammunition provides compelling evidence that the Ransom Rest meets important criteria for any device intended to measure recoil.
Footnotes
Footnote 1. A one-way analysis of variance (ANOVA) tests if there is a difference in gun movement between any of the charge weights used for that gunpowder. One look at Figure 2B shows there was, and that more gunpowder means more movement, but if there is too much overlap between the values they might not be statistically significantly different. A two-sample t-test asks if the data from two independent samples comes from the same population or different populations. In this example, it asks if the movement from two adjacent charge weights is "similar" or "different", and this also depends on how much the values overlap. The probability level (alpha) of post-hoc t-test pairwise comparisons was adjusted with a Bonferroni correction for multiple tests. A 0.05 alpha probability level was used and is adjusted as 0.05/the number of adjacent comparisons. The adjusted alpha levels were 0.025 with three charge weights (two comparisons) and 0.0167 with four charge weights (three comparisons). A one-tailed t-test was used since one predicts that more gunpowder produces more recoil (movement).
Footnote 2. A 0.05 probability was used. This means that if the correlation value is 0.549 or larger, there is at least a 95% chance that rocker arm movement correctly distinguishes between small differences in velocity. A one-tailed test criterion was used because I'm specifically testing for a positive correlation between rocker arm movement and velocity.
Shooting Times Ammo Reports
Pistol Powerhouse: The 9x23 Winchester
What's the Best Cartridge for Coyote Hunting?
Most fast varmint-type cartridges work just fine, but there are a few that excel. What cartridge would you choose for a dedicated predator-hunting cartridge?
Read the full article here.How to Reload 7.62x54R for Mosin Nagants
Handloading the 6.5mm Grendel
Sometimes you find a cartridge that really shines when it's handloaded, and it reinforces the notion that reloaders can improve the performance of their chosen cartridge and firearm. The 6.5mm Grendel is just such a cartridge.
Learn how to handload the 6.5mm Grendel.Essential Reloading Tools
Reloading tools are a lot like kitchen appliances; there are a lot that make life easier, but only a few that are absolutely necessary.
Find the best reloading tools.

